Linear Decision Boundary

Assume $h_{\theta}(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)$, and

$$\mathbf{\theta}=
\begin{Bmatrix}
\theta_0 \\
\theta_1 \\
\theta_2 \\
\end{Bmatrix}=
\begin{Bmatrix}
-3 \\
1 \\
1 \\
\end{Bmatrix}$$

where $g(x)$ is sigmoid function we had mentioned before. According to Wikipedia, the sigmoid function’s domain are all real numbers, with return value monotonically increasing most often from 0 to 1.

To predict $y=1$ (malignant tumor) ocurrancy, we set $h_{\theta}(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)\ge0.5$. It means that when the occurancy of malignant tumor is greater or equal to $50\%$, we tell the patients the tumor is predict to be malignant.

For $h_{\theta}(x)\ge0.5$, we obtain $x\ge0$, in other words,
$$\theta_0+\theta_1x_1+\theta_2x_2=-3+1*\theta_1+1*\theta_2\ge0$$
Here comes
$$\theta_1+\theta_2\ge3\tag{1}$$

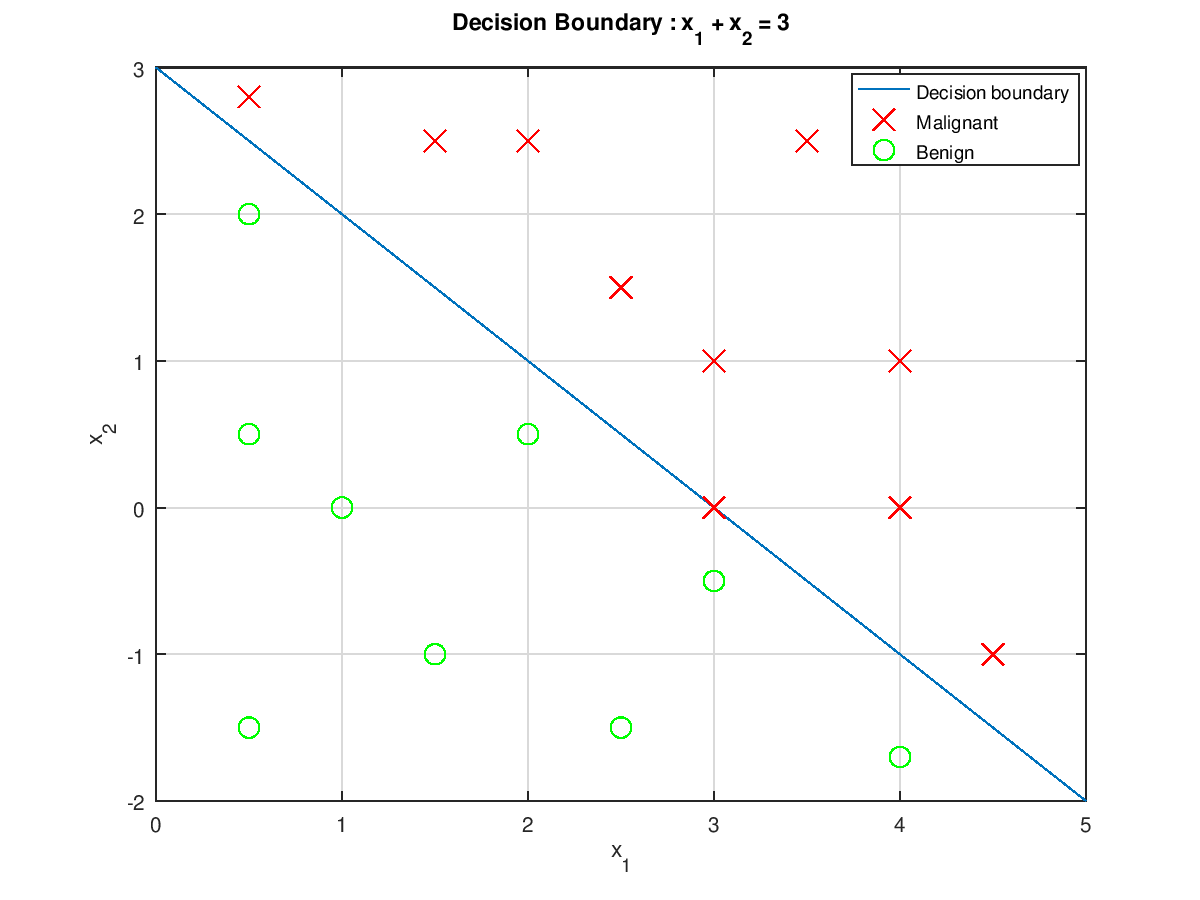
We can classify input data as:

$$x_1+x_2\lt3\Rightarrow h_{\theta}(x)\lt0.5\Rightarrow\text{benign}$$
$$x_1+x_2\ge3\Rightarrow h_{\theta}(x)\ge0.5\Rightarrow\text{malignant}$$

Non-linear decision boundaries

Assume
$$h_{\theta}(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)$$

if
$$\mathbf{\theta}=
\begin{Bmatrix}
-1 \\
0 \\
0 \\
1 \\
1 \\
\end{Bmatrix}
$$

we’ll predict $y=1$ if $-1+x_1^2+x_2^2\ge0$, i.e. $x_1^2+x_2^2\ge1$ is a circle decision boundary.

Decision boundaries is a property of how we choose $\mathbf\theta$(i.e. hypothesis $h_{\theta}(x)$), NOT of the traning data set. The training data set is not what we use to define the decision boundary, they may be used to fit the parameters theta.

How about the more complicate case…

$$h_{\theta}(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_1^2x_2+\theta_5x_1^2x_2^2+\theta_6x_1^3x_2+…)$$